الشكل المضلع هو الشكل ثنائي الابعاد و يمثل الشكل الاساسي لكل الاشكال الهندسية و هو يتكون من اتحاد عدد من القطع المستقيمة مكونة شكل مغلق , تمثل كل قطعة في المضلع ضلع , اما الزوايا فنجدها محصورة بين ضلعين من اضلاع المعين و تسمى زاوية المضلع و يوجد انواع من المضلعات منها المثلث و هو مضلع ثلاثي و المربع و المستطيل و متوازي الاضلاع و المعين و هو يمثل حالة خاصة من متوازي الاضلاع .
المعين .
المعين و ينطق بعين مضمومة و هو ضمن الاشكال الهندسية في الهندسة الاقليدية و هو من الاشكال الرباغية اي التي تتكون من اربعة اضلاع و تكون اضلاعه متساوية في الطول , كما يمكن ان نقول بانه عبارة عن شكل رباعي يتكون من مثلثين متساويي الساقين و لهما قاعدة مشتركة , ايضًا يمكن تعريفه بانه عبارة عن متواي اضلاع فيه كل ضلعان متجاوران متساويين .
خصائص المعين .
1- اضلاعه الاربعة متساوية في الطول و هو بتلك الخاصية يشترك مع المربع .
2- فيه كل ضلعين متقابلين متساويين .
3- فيه كل زاويتني متقابلتين متساويتين .
4- القطران في المعين متعامدان و ينصف كل منهما الآخر كما انهما يمثلان محوري التمثال ( التناظر ) للمعين .
5- كل قطر يقسم زاويتين متقابلتين الى زوايتين متساويتين و يقسم المعين الى مثلثين متطابقية و متساويين .
6- يضم المعين اربعة زوايا اثنان حادتان و اثنان منفرجتان .
7- يعتبر المعين حالة خاصة من متوازي الاضلاع و في حال كانت زواية المعين قائمة اصبح الشكل مربع .
8- المعين يعتبر راعيًا مماسيًا اي ان كل ضلع من اضلاعه يمكن ان يكون مماسًا لدائرة واحدة .
طرق حساب مساحة المعين .
هناك اكثر من طريقة او قانون يمكن من خلاله حساب مساحة المعين تتمثل في : –
اولًا حساب مساحة المعين بدلالة طولي قطريه .
يتم حساب مساحة المعين بدلالة طولي قطريه من خلال القانون الآتي : –
مساحة المعين بدلالة طولي قطريه = نصف حاصل ضرب طولي قطريه .
اي مساحة المعين = حاصل ضرب القطرين 2 .
مثال ( 1 ) : – معين طولا قطريه على التوالي 6 سم , 8 سم احسب مساحته .
الحل .
مساحة المعين = حاصل ضرب القطرين 2 او نصف حاصل ضرب طولي قطريه .
مساحة المعين = ( 6 × 8 ) 2 = 48 2 = 24 سم2 .
مثال ( 2 ) : – معين طول احد قطريه 5 سم و تبلغ مساحته 25 سم2 فكم يبلغ طول القطر الآخر .
الحل .
طول قطر المعين = ( 2 × المساحة ) طول القطر المعلوم .
طول القطر = ( 2 × 25 ) 5 = 50 5 = 10 سم .
ثانيًا حساب مساحة المعين باستخدام القاعدة و الارتفاع .
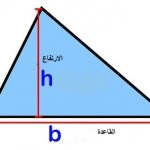
يتم ذلك من خلال قانون مساحة متوازي الاضلاع بما ان المعين عبارة عن متوازي اضلاع و يستخدم هنا ارتفاع المعين اي المسافة العمودية بين ضلعين متقابلين و احد احرف او اضلاع المعين و الذي يمثل القاعدة و يعبر عن القانون كالآتي : –
مساحة المعين = الارتفاع × القاعدة .
مثال ( 3 ) : – معين طول ضلعه 7 سم و ارتفاعه 10سم فكم تبلغ مساحته .
الحل .
مساحة المعين = القاعدة × الارتفاع .
مساحة المعن = 7 × 10 = 70 سم2 .
مثال ( 4 ) : – معين تبلغ مساحته 40 سم2 و طول ضلعه 10 سم فاوجد ارتفاعه .
الحل .
ارتفاع المعين = المساحة القاعدة .
ارتفاع المعين = 40 10 = 4 سم .
مثال ( 5) : – معين تبلغ مساحته 28 سم2 و ارتفاعه 7 سم اوجد طول ضلعه ( القاعدة ) .
الحل .
القاعدة ( طول ضلع المعين ) = المساحة الارتفاع .
القاعدة = 28 7 = 4 سم .
ثالثًا حساب مساحة المعين باستخدام حساب المثلثات .
يعبر عن قانون حساب مساحة المعين باستخدام حساب المثلثات في الآتي : –
مساحة المعين = مربع طول ضلع المعين × جا احدى زوايا المعين .
مثال ( 6 ) : – معين طول ضلعه 2 سم و قياس احدى زواياه 33 درجة اوجد مساحته .
الحل .
مساحة المعين = مربع طول ضلعه × جا ( 33 ) .
مساحة المعين = ( 2 × 2 ) × جا ( 33 ) = 4 سم2 .





أكتب تعليقك ورأيك